How To Do Substitution

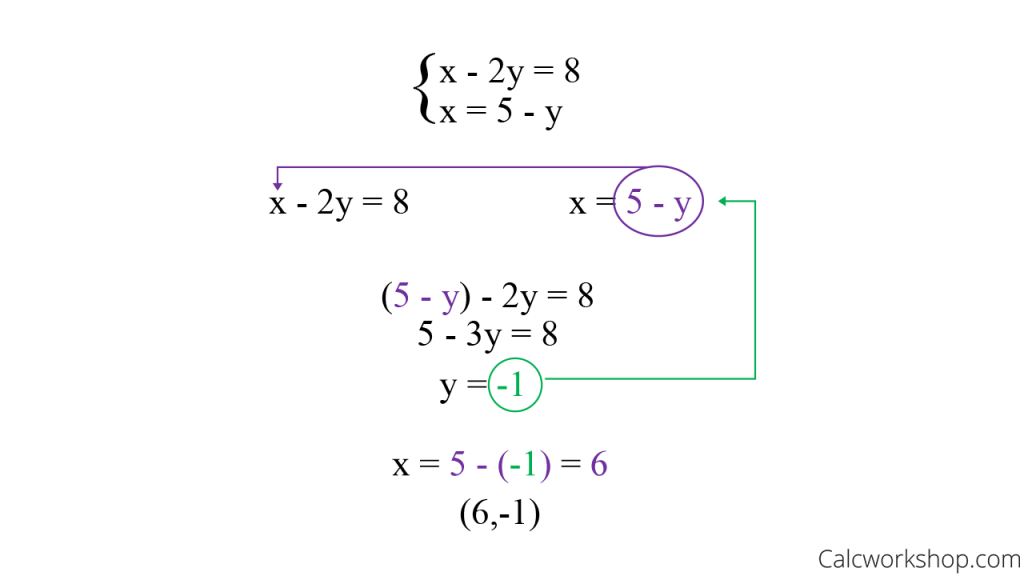
The method involved in substitution is called substitution, which involves solving one set of equations for two variables and plugging in values for those variables into their respective counterparts. Substitution is used to solve a number of problems involving multiple variables, such as the following: 1. Find the values of x and y for which the equation y = 2x + 3 is true.2. Solve the system of linear equations Ax + By = C.3. What is the slope of a line connecting the points (0, 0) and (1, 1)?4. How many times does the line intersect itself?5.

How do you solve by substitution?

” By choosing one equation and one variable, plugting the values of both into their respective equations, substituting the value of one for another, solving the resulting two equations for either one alone, or back resolving for whichever variable you chose. You then back resolve for whatever variable choice you made. This method is called “plugging and matching”. The method used here is to solve the equation for x, substitute the answer for y, solve again for z, repeat until you get to x. Once you have solved for X, you will have substituted the correct answer. If you are stuck on how to proceed, try pluggin’ in numbers and see if anything comes up. Sometimes you’ll get lucky and you might even get a solution. But if nothing comes out, don’t give up yet. Try plugin’ ’em in again and again until something works.

What is substitution example?

An Example of Substitutions: “I am going out tonight. I will be back in about an hour.”(Source 1): I am Going Out Tonight. ( source 2 ) I Will Be Back In About An Hour.This is how you say it. You are repeating what you have said before. To repeat what someone has said, make sure you follow the rules.

What are the 3 methods for solving systems of equations?

Graphene Substitution The graphene substitution method is quite similar in principle to graphhemy substitutions. Both involve the removal of a graphe from a graph, which is then replaced with the corresponding grapheet. Whereas graphing substitution entails the complete replacement/removal of every graphet, i.e. graphes, with graphens, likewise, there are times when graphem substitution becomes necessary. For instance, suppose we have a simple graph consisting of two nodes and three edges. We can replace the node with two graphs, namely, a pair of adjacent graphests connected by a common edge. Similarly, we can remove the edge and replace it with four graphis, viz., two adjacent pairs of neighboring graphtes connected together by an edge, two pairs between two neighboring edges connected via a path, or two paths connecting two vertices. If we want to add a fifth edge to our graph without affecting the rest of our structure, say, by adding a fourth edge between the two remaining nodes, such a substitution can easily be made. Likewise, removing an existing edge from our network and replacing it either with an adjacent pair or a second pair results in identical results. Finally, assuming that we wish to create a new graph containing a third node and a sixth edge connecting the newly created node to itself, once again we need to perform a similar substitution procedure. To make matters worse, depending on how we choose to proceed, both the number of substituting graphents and the total number required to completely replace our original network can vary greatly. Therefore, before attempting to make a final substitution using graphin substitution techniques, let us first discuss the pros and cons of this technique. Pros of Graphin Substitutes The main advantage of graphin substitution methods is that they allow us to obtain a variety of different structures from the same graph within a short period of time. Moreover, because of its versatility, these methods can provide us with numerous options for creating new graphs. Another important advantage is the ease with which we may combine different types of graphs into a larger structure. By combining different graphs together, e.g. by joining two or more graphs along a line, additional structural possibilities are opened up. Additionally, simply by changing the position of one or few of those joined graphs relative to each other, significant changes in overall structure can occur. Cons of Gropin Substitutons The major disadvantage of these substitution procedures is their complexity.

Why is substitution method better?

: Substitution gives us this benefit since we don’t have any extra variables to worry about. When we substitute, all we have left is the variable we’re interested in. If we wanted to change the value of x, say, to 2, our equation would look like this: f (x)=2. Substitute x = 2 and you’ll get -2a + 2a = 0. So now we’ve got a new equation: -a+(2*a) =0. Solving this equation will give us a solution of (-a)+a=0; therefore, x must be equal to 1. And that’s it! This is a great way to come up with solutions to equations. You can use this method to generate all sorts of interesting answers to questions like “What is x?” or “How many times do I have x?”, etc. As a bonus, you might even be able to figure out the answer to your own equation.

Which is the best example of substitution?

Answer : The answer is both. Option C is a movie theatre which is owned by the same company. This means that there is no way for someone to switch theaters without changing the name of their ticket. On the other hand, option D is an independent movie house which requires a change of name. There is nothing stopping someone from buying a ticket to an option B movie and switching to option A after seeing the film. However, this is unlikely to happen since the majority of movie theaters are owned and operated by a single company and therefore cannot be changed without a major change in ownership. So, unless you want to go to two movies in one day, you will probably opt for option E. But again, even if we were to say that option F is preferable, I would still choose option G.

What are substitution sentences?

Substitute in grammer is replacing a previous word with another word in place of it. For example, one would replace “one” with ‘one’‍; do with ‘do’; this means that the former word is being replaced with the latter. This is done to prevent repetition of words. Another example is „this‟ which is substituted with “that” in ‚this is‌. Another example would be ‛the‖ which replaces †with ‡.

What is substitution method?

Substitution method means the algorithm to calculate the solution of simultaneous equations using the substitution technique. This method uses the following steps: 1. Solve the equation by substitution. For example, if we want to find the values of x and y, we substitute x = 2 and Â= 1 into the original equation (x + y = 3). 2. Find the solutions of all the variables. If we have two equations, say, xy = 5 and xz = 6, what are the possible values for x, y and z? 3.

What are the 3 types of equations?

Two of them are point sloped equations, which are used to describe the relationship between two variables. And the third one is called slope intercept form equation, whose purpose is to determine the slope of a line. Point sloping equations are usually used when we want to know the value of one variable at a point, while slope interception form is used for determining the position of an unknown point along a curve.

What is the easiest way to solve system of equations?

This Technique involves solving the system separately.For example say, let us assume that we have the following equation: (x1+x2+…+nxn)^m=c.Here,we have n=3,m>1,and c=1.We can solve this system by substitution technique.Let us suppose that the roots are 1,2,3.By substituting x1=2;x11=10;etc,you will arrive at the same result.EvaluationMethod :-This technique involves evaluating the values of certain poisson brackets.In our case,the poisition brackets are (p1)(p2)(…)(pn)where p1,…,pn are the coefficients of power series expansion of f.If you want to know the exact value,then you need to evaluate the poiitions.The exact values are given by the formula: [P(a)]=[P]/[a] where P is the coefficient of corresponding power of exponentials.Note that there are many ways to calculate the evaluations.One way is to use the power sum theorem.Another way to do it without using the Power Sum Theorem is by using a computer.Both methods are available in many programming languages.There are also many books on this topic.Please check out my website for more details.http://www.math.unimelb.edu.au/~majid/maths/ paraphrasing: Substituting a variable in two equations gives you a third equation. So, when you substitute x for y, you’re actually replacing x by y twice. You can also write this as x*y. If you don’t understand this, please check my book. article: When you have a list of numbers, what is meant by “adding” them? Paraphrasme: Adding numbers means adding the digits of each number. e. g. 10 + 11 = 12.Adding the first digit of 10 and the second digit 8 gives 10+8 =12.Add the last digit 7 and make it 10. Thus, 10 * 7 = 10. article: How to find the sum of all the numbers in an array? paraphra: To find out how many numbers are in any given array, simply count the elements in that array. Let’s say you’ve got an Array of integers, say {1..10}.

What is the easiest way to solve linear equations?

What is easier than graphing systems of equations is grapching them as lines. This is what you do when you want to find points where two lines meet. You simply graph the equations as straight lines and see where they intersect (or don‘t). The easiest method to solving linear algebraic equations involves graphed solutions. To solve an equation such as x = 2x + 3, you need to plot the equation on a graph and determine the intersection of those two curves. If you grapch this equation, there will be a point where both lines cross. There are many ways of grapcheting equations, including grapheming them in either slope/intersection form or in standard form.